Silverback9

오늘도 x,y 축 좌표점을 사용하는 데카르트 좌표계(Cartesian Coordinate System)와 빗변 길이와 각크기를 사용하는 극좌표(Polar Coordinate System)에 익숙해 지는 연습을 해 보겠습니다~^^*

아래 동영상 강의를 클릭하셔서, 11:25까지 보시면 오늘 공부 끝~~^^*

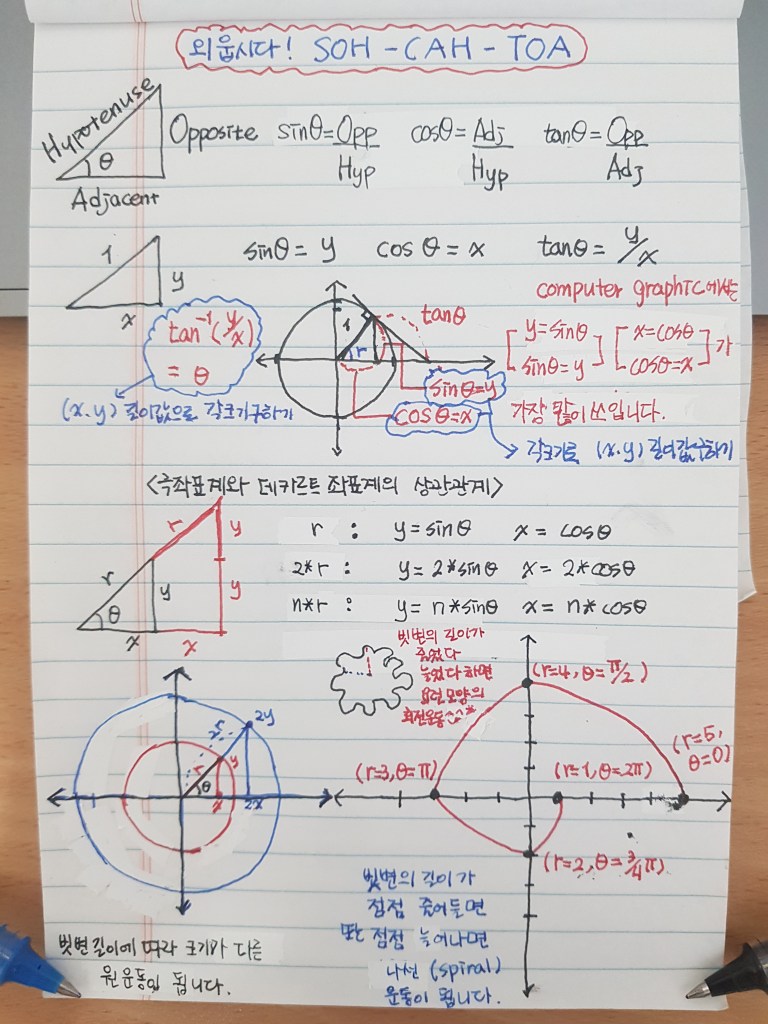
사람인 우리는, 회전운동을, 빗변 길이와 각크기를 사용하는 극좌표계(Polar Coordinate System)를 사용하여 구상하는 것이 편하겠지요^^* 그러나 컴퓨터는, 회전운동을, 캔버스 화면 위 x,y 축 좌표점을 사용하는 데카르트 좌표계(Cartesian Coordinate System) 위에서만 작업을 해 낼 수 있어요~^^*.

그래서!!

우리는 지금까지 데카르트 좌표계(Cartesian Coordinate System)와 극좌표계(Polar Coordinate System)를 자유롭게 넘나들 수 있는 연습을 한 것 같아요~. 벡터의 x,y 축 길이값으로 각크기를 구하기도 하고, 각크기로 벡터의 x,y 축 길이값을 구하는 활동을 하기도 했어요~^^* 그리고, 삼각함수는 이 활동들의 근간이 되어 주었지요?

그래서!!

한 번 더 삼각함수 복습하고 가실게요~~~~^^*

오늘은 강의 동영상의 예시 작품의 내용에 push()____pop() 구조 사용을 더하여, 다양한 색깔의 행성이 다양한 크기의 궤도 위를 다양한 방향으로 다양한 크기의 회전각 운동을 하는 것을 표현하는 프로그램을 만들어 보겠습니다.

코드 안의 주석 내용을 참고해 보셔도 좋겠지요~^^*

let rAngle = 0;
let gAngle = 0;
let bAngle = 0;
let r = 75;


//빨간 행성, 초록 행성, 파란 행성의 회전각 및 궤도 기본 반지름은 글로벌 변수로 만들겠습니다. 언제라도 수정하기가 편하겠지요? 

function setup() {
  createCanvas(400, 400);
}

function draw() {
  background(0);
  stroke(255);
  strokeWeight(4);
  noFill();
  translate(200,200);
 
  
  //중간 크기의 궤도 위에 빨간 행성이 시계방향으로 돌아갑니다. 
  push();
  circle(0,0, r*2);
  //기본 궤도를 그립니다.  
  
  strokeWeight(32);
  stroke(255, 0, 0); //빨갛네요!
  let rX = r*cos(rAngle);
  let rY = r*sin(rAngle);
  point(rX, rY); //궤도 위에 빨간 동그라미를 콕 찍어 봅시다~ 
  rAngle += 0.01;
  //시계방향 회전운동합니다. 
  pop();
  
  
  
  //가장 큰 크기의 궤도 위에 초록 행성이 반시계방향으로 빠르게 돌아갑니다. 
  push();
  circle(0,0, r*4);
  //기본 궤도의 2배 크기인 궤도를 그립니다. 
  
  strokeWeight(32);
  stroke(0, 255, 0); //초록초록하네요!!
  let gX = 2*r*cos(gAngle);
  let gY = 2*r*sin(gAngle);
  point(gX, gY);//궤도 위에 초록 동그라미를 콕 찍어 봅시다~
  gAngle -= 0.02;
  //다른 동그라미에 비해 2배속으로, 반시계방향 회전운동합니다. 
  pop();
  
  
  
  //가장 작은 크기의 궤도 위에 파란 행성이 반시계방향으로 돌아갑니다.  
  push();
  circle(0,0, r);
  //기본 궤도의 1/2 크기인 궤도를 그립니다.  

  strokeWeight(32);
  stroke(0, 0, 255); //새파랗네요!!
  let bX = r/2*cos(bAngle);
  let bY = r/2*sin(bAngle);
  point(bX, bY); //궤도위에 파란 동그라미를 콕 찍어봅시다~
  bAngle -= 0.01;
  //반시계방향 회전운동합니다. 
  pop();
   
  
}

이것을 클릭하여 sketch.js 파일을 열어 코드를 살펴 보셔요~^^* 그리고 삼각형을 눌러 서로 다른 크기의 궤도 위를 서로 다른 방향과 회전각으로 운동하는 서로 다른 색깔의 행성을 만나 보실까요~^^* 깔끔한데 예쁘죠~~^^* 넵, 종료는 사각형~~~^^*

오늘은 반듯한 모양의 원운동을 표현해 보았습니다~~~^^* 서로 다른 모습과 서로 다른 궤도에서 움직이고 있지만 함께 노래하고 춤추며 멋진 공연을 만들어 내듯, 오늘도 함께 공부 해 주셔서 감사합니다~~^^*.

내일은~~~ 음~~~내일은~~~아직 노트 정리 내용이 끝나지 않았죠~~~^^? 그렇죠! 나선형 운동을 표현해 볼게요~~~^^* 오늘 공부가 끝나도 끝나지 않은 듯한 여운과 기대를 에너지 삼아 힘찬 하루 보내시고요~~~^^* 우리 내일 또 만나서 코딩 공부 함께 해요~~~^^*

네, 꿈은 이루어 집니다!!!