Silverback9

오늘은 Java에서 각의 크기가 클수록 사인함수의 계산처리 과정이 길어지는 이유를 공부해 보겠습니다~^^*

본격적인 공부에 앞서, 아페타이져로~^^* 사인곡선에 대해 복습 한 번 하고 시작할게요~^^* Sine이라는 말이 생겨나게 된 과정도 설명이 되어 있는 동영상 한 번 같이 볼까요~~^^*

Sine 의 어원을 정리해 보았습니다~^^*

다른 언어는 사인 함수의 경우 (1) 각크기에 따라 유사치 값을 정리한 테이블을 미리 작성하여 두고, 해당 각크기의 사인 함수가 호출되면, 그 해당값을 테이블에서 찾아 반환하거나. (2) 각이 0에 가까울 정도로 아주 작은 경우는 sin(x) = x 로 처리하고 더 큰 각의 경우 테일러 시리즈를 사용하거나, (3) 하드웨어적으로 기계어 연산을 하여 값을 도출하는 경우가 있습니다. 그러나, Java의 경우 모든 각크기에 대해 테일러 시리즈를 사용하여 값을 소프트웨어적으로 계산하여 반환합니다. 그런데 각의 크기가 크면 사인함수 처리시간이 점점 길어진다고 합니다.

테일러 시리즈에 따르면,

sin(x) = x – (x^3)/3! + (x^5)/5! – (x^7)/7! + ……+ (-1)^n*(x^(2n+1)/(2n+1)!

이 됩니다.

근사치값을 거칠게 잡기 위해 항의 갯수를 작게 잡더라도 ( n의 크기를 작게 잡더라도 ), x^(2n+1)의 관계, 즉 x가 밑이고 (2n+1)이 지수인 관계, 때문에, x를 (2n+1)번 반복해서 곱하는 과정이 필요합니다.

x의 값이 커지면, x를 (2n+1)번 반복해서 곱하는 과정이 매우 큰 값을 다루게 됩니다. 또한 근사치값을 정교하게 하기 위해 항의 갯수를 어느 정도 적정한 갯수로 잡다보면, 연산과정도 길어지게 되겠지요.

그래서 Java의 경우 sine 함수의 값을 구할 때, 각의 크기가 커지면, 다루는 수치값도 크고 계산 업무량도 많아져서 자연스럽게 계산시간도 길어지는 것 같습니다.

특히, 컴퓨터는 곱셈 연산이 따로 있는 것이 아니고, 덧셈의 반복하는 것이라서, 연산과정이 매우 길어질 수 있습니다. 자기 자신을 (2n+1)번 곱한다는 것은….음….연산과정이 엄청나게 길어질 수 있겠네요.

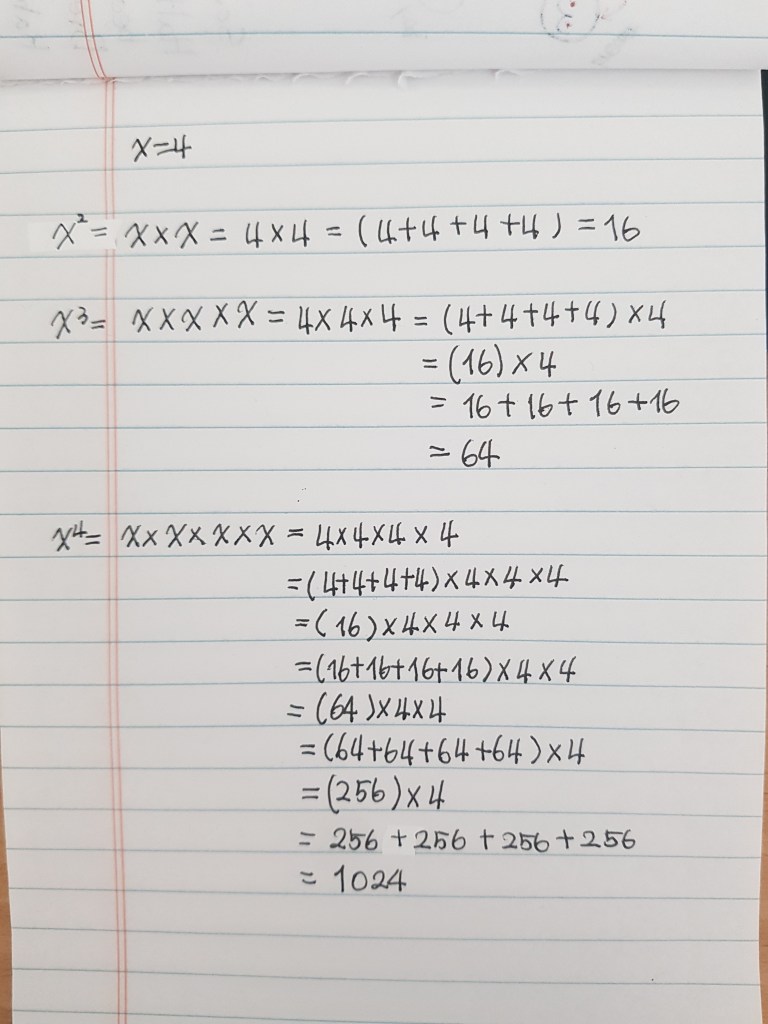
그리고 보통 테일러 시리즈를 이용해 항의 갯수가 13개인 다항식으로 계산하는 알고리즘을 쓰는 것 같습니다. 그러면…와우…정말 계산 업무량이 많을 것 같아요!

우리는 이제 훌륭하신 테일러님을 만나보겠습니다~^^*

테일러 시리즈를 시각적으로 설명하는 동영상도 보실까요~^^* 그림만 보시면 되어요~~^^* 시청자 모드로 가볍고 편안한 마음으로 보셔요~~^^*

어제 만든 프로그램의 원의 팽창수축 반복운동이 시간이 지날 수록 왜 더 느려지는지 알게 되어 기분이 개운합니다~^^* Java도 Tate처럼, 당찬 꿈을 안고 느리게 성장하기를 감내하는 14살 소녀처럼 순수한가봐요! 오직 소프트웨어의 힘만으로! 각크기와 상관없이! 순수하게 테일러 시리즈만을 이용해서 사인(각크기) 값을 계산해 내는 뚝심이 느껴지네요!!!

개운한 기분으로 점심 맛있게 드셔요~~~^^*

오늘도 함께 코딩 공부해 주셔서 감사합니다~~~^^*

우리 내일도 함께 코딩공부 할까요~~~^^*

넵!!! 꿈은 이루어 집니다~~~!!!