Silverback9

오늘은~~^^*

어제 광복절 결심을 실천하고 있습니다~~^^*

오전 일정 전에 미리 근처에 도착해서, 시원한 공간에서 코딩공부를 시작하였습니다~~^^*

YEAH~~!!! 성공~~~!!!

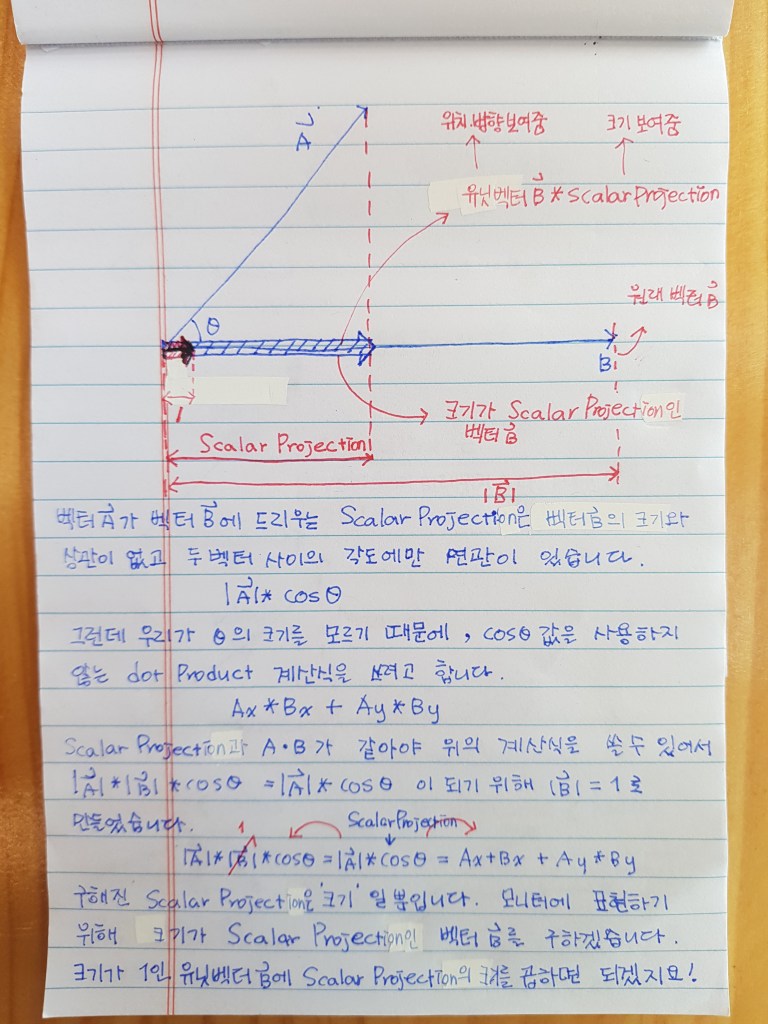
지난 14일 벡터 B의 크기를 1로 줄여 유닛벡터로 만든 후, 벡터 A가 이 유닛벡터 B에 드리우는 Scalar Project를 벡터 A와 유닛벡터 B의 Dot Product로 구하였지요~~^^*

그런데 이 Scalar Project는 ‘크기 magnitude’이기 때문에 컴퓨터 화면에 표현할 수 있는 위치좌표도 방향도 가지고 있지 않아요. 그래서 우리 눈에 보이지 않아요~~^^*

이 Scalar Project를 컴퓨터 화면에 표현해 보고 싶다면 어떻게 하면 좋을까요~^^*

어머 근데요!!!

벡터 B의 유닛벡터는 벡터 B의 방향성과 그에 따른 위치 좌표를 가지고 있는데, 크기가 1일 뿐이잖아요~~^^*

그렇다면!!!

아하!!! 그렇죠!!!

이 유닛벡터 B에 Scalar Project를 곱하면, 벡터 B의 방향성을 가지고 Scalar Project의 크기에 따른 위치좌표를 가진 벡터가 만들어 지겠네요!!!

크기가 Scalar Project인 벡터 B!!!

그러면~~ 벡터 B위에 벡터 A가 드리우는 그림자를 시각적으로 표현할 수 있을 것 같아요!!!

저의 유추과정을 노트에 기록해 보았습니다~^^* 함께 살펴봐 주시면 감사하겠습니다~~^^*

이 알고리즘에 따른 우리들의 “오늘의 핵심코드!”는~~~^^*

function vecterPorjection(a, b) {  

let bCopy = b.copy(b).normalize();
//벡터 B를 복사해서 원본은 따로 두겠습니다. 우리는 복사본을 가공해 봅시다~!
//벡터 B 복사본의 크기를 1로 만들어 유닛벡터 B를 만들어 봅시다~!

let sp = a.dot(bCopy);
//벡터 A와 유닛벡터 B의 dot product를 구해봅시다~!
//이것은 벡터 A가 벡터 B에 드리우는 Scalar Project이기도 합니다!

bCopy.mult(sp);
//Scalar Project는 '크기'라서 단독으로는 화면에 표현할 수 없습니다.
//벡터 B의 방향성을 가지고 '크기 1'에 따른 위치좌표를 가진 유닛벡터 B에 '크기 Scalar Product'를 곱해 봅시다! 

return bCopy;
//이제 bCopy는 벡터 B의 방향성을 가지고 크기 Scalar Project에 따른 위치좌표를 가진 벡터가 되었습니다!  
//bCopy를 뿌듯한 마음으로 return합시다!

}

와우!! 며칠 연속으로 곱셈을 자주 만나게 되네요!!

그래서인가요~~!!!

요즘 어린이들은 9단을 넘어서 12단까지 곱셈 연습을 하네요~~!!!

우리도 12단 도전~~!!!

오늘도 저와 함께 핵심 코드 원리 공부를 해주셔서 감사합니다~!!!

내일은 우리 이 Scalar Project를 화면 속에서 만나 볼까요~~?

네~~!!! 꿈은 이루어 집니다~~~!!!!