Silverback9

오늘은 2 Dimensional Elastic Collision 2차원 탄성 충돌의 순간을 포착하기 위해서 두 입자 사이의 거리를 조정하는 코드를 공부해 보기로 할게요~^^*

우리가 어떤 두 물체가 접촉했다는 것을 어떻게 알 수 있을까요?

음….그러네요! 네! 맞는 것 같아요!

두 물체의 반지름의 합이 두 물체의 거리와 같을 때 두 물체가 접촉했다고 볼 수 있겠어요!

그 순간의 접촉면의 좌우로 뻗은 tangent line과 위아래로 뻗은 normal line을 우리가 그림으로 그려보았었지요~^^*

그런데~~접촉한 순간을 정확하게 포착하기란 쉽지 않을 수도 있을 것 같아요…

p5.js 의 draw() 함수가 무한 반복하면서 두 물체의 위치 그리고 그에 따른 둘 사이의 거리를 시시각각으로 점검할 수는 있지만, 그것이 꼭 실시간 점검은 아닐 수 있기 때문이겠지요…?

시간차가 발생하기 때문에, 어떤 경우에는, t1에서는 접촉하지 않았는데, t2에서는 이미 접촉하고 이동을 계속해서 서로의 영역이 겹쳐진 부분이 발생할 수도 있을 것 같아요.

그런데, 우리는 접촉면의 좌우로 뻗은 tangent line의 방향을 가진 유닛벡터가 필요하기 때문에, 접촉의 순간을 다시 재연해서 멈출 필요가 있을 것 같아요.

그렇죠!

t1에서는 접촉 전, t2에서는 이미 접촉 후 영역 겹침이 발생했다면, 두 물체를 뒤로 움직여 접촉상태로 만들면 어떨까요?

하나의 물체를 this 다른 하나의 물체를 other로 표현해 볼게요.

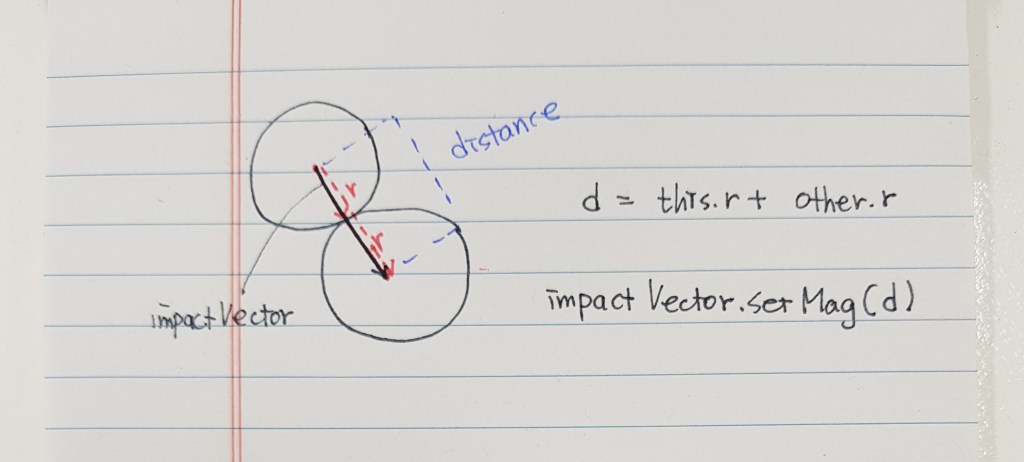
두 물체가 서로 다가가서 부딪치는 순간 발생하는 충격 벡터를 구해 볼게요. 이것은 두 물체의 질량 중심 사이를 잇는 선의 길이와 방향을 가진 벡터일 것 같아요.

    let impactVector = p5.Vector.sub(other.position, this.position);

그러고 보니, 두 물체 사이의 거리도, 두 물체의 질량 중심 사이의 길이를 말하는 것이네요.
그래서 충격 벡터의 길이값을 거리로 볼 수 있겠어요.

let d = impactVector.mag();

두 물체 사이의 거리가 두 물체의 반지금의 합보다 작은 경우를 우리 함께 고민해 볼까요?

if (d < this.r + other.r)

두 물체 사이의 거리가 두 물체의 반지름의 합보다 작다면, 충돌 후 영역이 겹쳐지고 있다는 의미이니까, 이때 두 물체를 뒤로 옮기도록 할게요. 두 물체 사이의 거리가 두 물체의 반지름의 합과 같도록요~~^^*

(1) 두 물체의 영역이 겹쳐진 길이를 파악해 볼까요~^^*

두 물체의 거리에서 두 물체의 반지름의 합을 빼 볼게요. 마이너스 값이 나올텐데요.

이것이 나중에 두 물체를 뒤로 빼는 역할을 하게 될 것 같아요.

let overlap = d - (this.r + other.r);

(2) 두 물체를 옮길 방향은 충격 벡터와 같은 선상에 있어야 되겠지요~^^*

 let dir = impactVector.copy();

(3) 두 물체의 영역이 겹친 길이의 반만큼, 두 물체가 자신의 이동방향에서 뒤로 물러서도록 할까요~^^*

dir.setMag(overlap * 0.5);

(4) 한 물체 this의 이동방향은 충격 벡터의 방향과 같기 때문에, 뒤로 물러서기 위해서는, 마이너스 값의 overlap을 그대로 더하면 될 것 같아요. (ex, +(-1) = -1)

this.position.add(dir);

(5) 다른 한 물체 other의 이동방향은 충격 벡터와 반대방향과 같기 때문에, 뒤로 물러서기 위해서는 마이너스 값의 overlap을 뺄셈을 해서 (ex, -(-1) = +1) 플러스 효과를 주면 될 것 같아요.

other.position.sub(dir);

이제, 한 물체 this는 충격벡터 방향에서 반대방향으로 반발짝 움직이고, 다른 한 물체 other는 충돌벡터의 방향으로 반발짝 움직여, 두 물체가 딱! 접촉하는 바로 그 순간!이 될 것 같아요!

(6) 이제, 두 물체 사이의 거리는 두 물체의 반지름의 합과 같겠네요! YEAH!

 d = this.r + other.r;

(7) 두 물체가 접촉한 순간이 재연되었으니, 이때의 두 물체 사이의 거리를 충격 벡터의 길이값으로 정하도록 할까요~~^^*

 impactVector.setMag(d);

네~^^* 두 물체가 충돌 후 영역이 겹쳐진 시점이라면, 두 물체가 서로 접촉하는 순간으로 되돌리는 작업을 해 보았습니다~~^^*

근데, 그림이 곁들여 진다면 좀더 그 과정이 이해하기 쉬울 것 같아요~~^^* 충격 벡터의 방향이 어느 방향이지??? 살짝 아리송하실 수도 있을 것 같아요~~^^*

그림으로 표현하는 작업을 오후에 보완해 보도록 할게요~^^* 지금은 저도 오늘의 일정을 시작해야 해서요~~ 오후에 보충해 놓을테니, 햇살이 순해지는 저녁에 다시 확인해 보시면 감사하겠습니다~~~^^*

네^^* 오후에 다시 돌아올게요~~^^*

멋진 아침! 보내시구요~~ 곧 또 다시 만나요~~~^^*

네~~^^* 즐거운 하루 보내셨나요~^^*

그림 그려서 돌아왔습니다~~~^^*

물체 other의 위치 벡터에서 물체 this의 위치 벡터를 뺏을 때 물체 this에서 물체 other로 향하는 벡터 impactVector가 생성됩니다~

이것을 이해하면, 물체 this가 뒷걸음치는 것은 impactVector의 마이너스 방향, 물체 other가 뒷걸음치는 것은 impactVector의 플러스 방향이 된다는 것을 이해할 수 있게 되는 것 같아요~~^^*

반걸음 뒷걸음 치는 벡터 dir이 이미 impactVector의 마이너스 방향이기 때문에,

물체 this는 dir를 더하고 (마이너스 * 플러스 = 마이너스)~~

물체 other는 dir을 빼면 (마이너스*마이너스 = 플러스) 될 것 같아요~~^^*

아직 다가가지 못했다면 한 발짝 앞으로, 이미 지나쳐 버리고 있다면 한 발짝 뒤로 움직여, 마침내 우리는 서로에게 닿습니다~~^^*

오늘 저와 함께, 두 물체가 서로 겹쳐있는 시점에서 두 물체가 딱 맞게 서로 닿고 있는 시점으로 되돌아가는 코드를 공부해 주셔서 감사합니다~~^^*

내일은 이렇게 맞닿게 된 두 물체 사이의 충격 벡터의 작용으로 인한 두 물체의 움직임을 표현하는 코드를 우리 함께 공부해 볼까요~~^^*

오늘 저녁도 즐겁게 오늘 밤도 편안하게 보내시고요~~^^*

네~~!!! 꿈은 이루어 집니다~~!!!